[역전파법(backpropagation)]

 

안녕하세요 개알못입니다~

저번 SGD 시리즈에 이어 이번에는 역전파법에 관하여 이야기 하겠습니다 :)

---

SGD 시리즈에서 나와 있다시피, 앞먹임 신경망(feedforward neural network)에서는 weight와 bias에 대한 오차함수의 미분을 계산해야합니다. 역전파법(backpropagation)은 이러한 미분을 효율적으로 계산하는 방법입니다. 앞으로 역전파법과 계산식 유도에 대해 알아보겠습니다.

 

 

1. 역전파법을 왜 사용하는가?

 

예를 들어 샘플 Xn에 대한 제곱오차를 (식 1)라 할 때,

 

(식 1)

 

(식1)를 l번째 층의 가중치 W(l)의 한 성분인 Wji로 미분하겠습니다. En을 편미분 하면 (식 2)이 나옵니다.

 

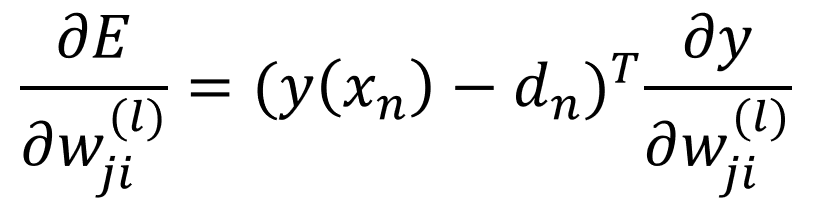
(식 2)

 

여기서 우변의 두번째 항은 미분형태 이므로 다시 한번 구해야됩니다. 그러기 위해 y(x) 안에 Wji가 얼마나 들어있는지를 알아야 합니다. 이는 미분 연쇄법칙을 통해 살펴보면 아래 (식 3)과 같습니다.

 

(식 3)

 

이렇게 되면 계산 비용이 급격하게 증가하므로, 단순히 미분 연쇄를 하는 것은 바람직하지 않습니다. 이를 해결하는 것이 바로 역전파법(backpropagation)입니다.

 

 

2. 2층으로 구성된 신경망 계산

(그림 1)

 

역전파법을 설명하기 전해 표기를 간단히 해보겠습니다. (그림 1)을 보시면 항상 +1을 출력하는 0번째 노드를 각 층마다 추가하였습니다. 이는 가중치 W0j를 bj로 표현한 것입니다. 더불어 l층의 노드의 입력에 l-1층의 0번째 유닛이 항상 1로 합니다. 어렵게 설명했지만 이를 식으로 나타내면 아래와 같습니다.

 

(식 4)

 

이제 그림 1의 2층 신경망을 회귀 문제에 적용하여 출력층의 활성함수를 항등사상로 설정합니다. 이때 신경망에서는 입력 x = [x1 x2 x3 x4]T가 출력 측으로 전파됩니다.

 

입력층의 출력을 아래와 같다고 할 때,

입력층의 출력

중간층의 출력은 (식 5)와 같습니다.

(식 5) : 중간층의 출력

 

출력층의 활성화 함수를 항등사상으로 했기에 (식 6)이 나옵니다.

(식 6) : 출력층의 출력

처음 조건에 회귀문제라고 했으므로, 오차함수로 제곱오차(식7)를 골랐습니다.

(식 7)

 

이때 (식 2)에서 한 것처럼 가중치에 대한 미분을 각각의 층에서 해주겠습니다. 먼저 l=3일때 부터 살펴보겠습니다.

 

(식 8) : 출력층 기울기에 대한 미분

여기서 (식 8) 우변의 2번째 항은 (식 6)을 통해 미분하자면 두번째 Zi만 남고 나머진 0입니다. 즉 아래처럼

표현할 수 있습니다. 이를 (식 8)에 다시 대입하면 (식 8)과 같습니다.

(식 8)

 

 

그다음 중간층의 기울기에 대한 미분을 계산하겠습니다. 

 

(식 4)에서 중간층이 l=2이므로 그대로 대입을 하면 아래의 식이 나옵니다.

(식 9)

그러므로 En을 l=2인 uj로 미분하여 연쇄법칙을 적용하면 (식 10)처럼 됩니다.

(식 10) : 중간층의 기울기에 대한 미분

(식 10) 우변의 2번째 항은 (식 9)를 활용하여 아래와 같이 표현할 수 있습니다.

식 10 우변의 2번째 항

 

그 다음 (식 10) 우변의 첫번째 항을 살펴보겠습니다. 

 

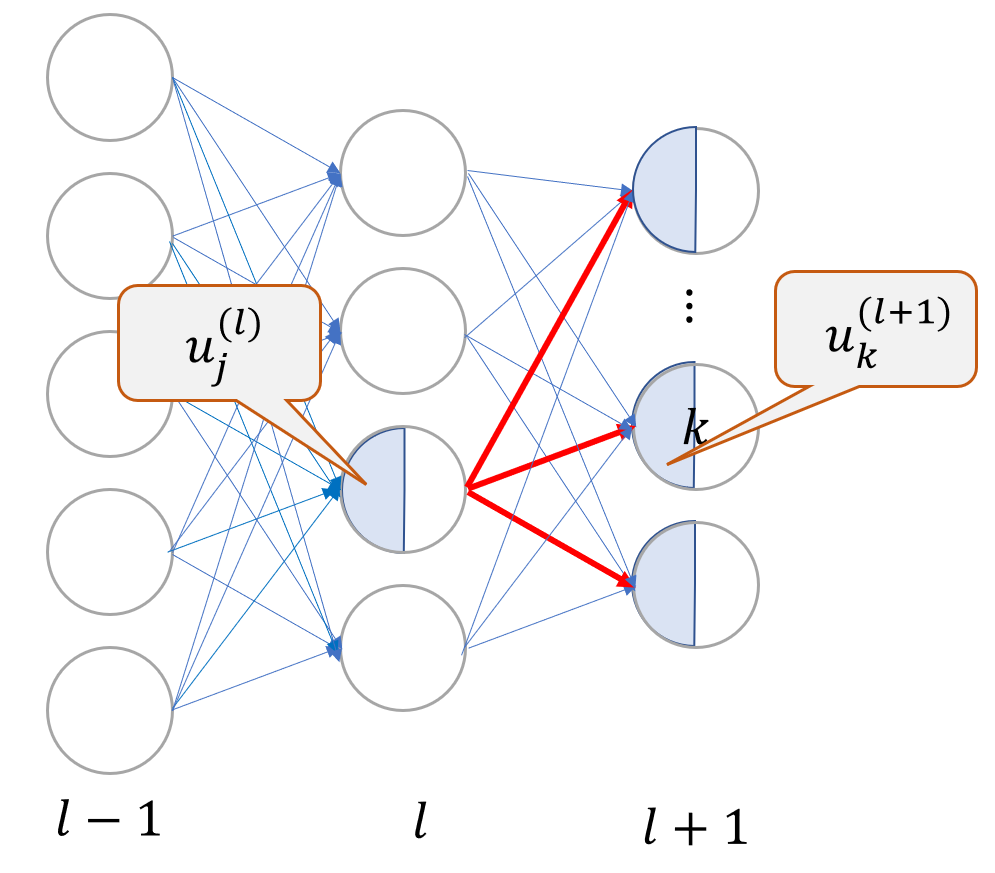
(그림 2)

(그림 2)에서 보시는바와 같이 중간층 노드 j의 입력 uj는 출력층의 각 노드 k(k=1, 2, 3)의 총 입력 uk에 영향을 미칩니다. En의 uj에 대한 미분은 연쇄법칙을 적용하여 출력층의 셋 노드에 대한 합으로 나타낼 수 있습니다.

(식 11)

(식 11) 우변의 1번째 항은 (식 12)를 활용하여 미분해 보면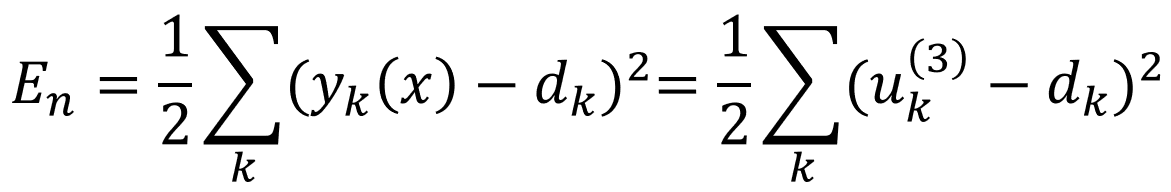

(식 12)

아래의 (식 13)을 쉽게 구할 수 있습니다.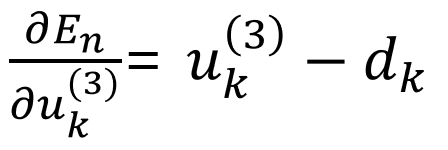

(식 13)

(식 11) 우변의 2번째 항은 (식 4)에서 l=3을 대입한 (식 14)를 이용합니다.

(식 14)

이를 이용해 다음을 계산하면 아래(식 15)와 같습니다.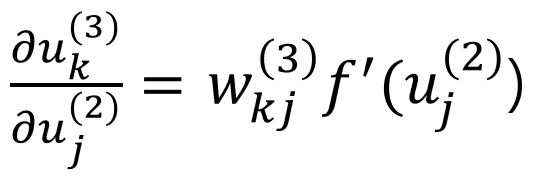

(식 15)

이제 다 왔습니다..!!! 처음 구하고자 한 (식 10) 우변의 각각의 값들을 다 대입하면 최종적으로 (식 16)이 나옵니다.

(식 16)

 

 

3. 다층 신경망으로 일반화

 

앞서 본 2층 신경망의 경우 (식 8)과 (식 16)로 계산하였습니다. 이제 임의의 층수를 갖는 신경망으로 확장하겠습니다. 단지 2층 신경망의 중간층 가중치에 대한 계산을 일반화할 뿐입니다.

 

(그림 3)

(식 10)을 l번째 층의 가중치에 대한 식으로 일반화를 해보면 아래(식 17)와 같다.

(식 17)

우선 (식 17) 우변의 1번째 항을 살펴보면, (그림 3)와 같이 l층 노드 j 입력의 변동이 En에 미치는 영향은 해당 노드 j의 출력 zj를 통해 l+1번째 층의 각 유닛 k의 총 입력 uk를 거칩니다. 이를 연쇄법칙을 적용하여 아래 식(식 18)과 같이 분해 할 수 있습니다.

(식 18)

이때 (식 18)은 양변에 l번째, l+1번째 층의 입력에 대한 미분이 있으므로, 이를 '델타'라고 부르고 (식 19)으로 표현합니다.

(식 19) : 델타

델타는 각 층 l의 각 노드 j마다 정의됩니다. 이후 (식 4)를 토대로 (식 20)를 만들 수 있고, (식 21)를 도출해낼 수 있습니다.

(식 20)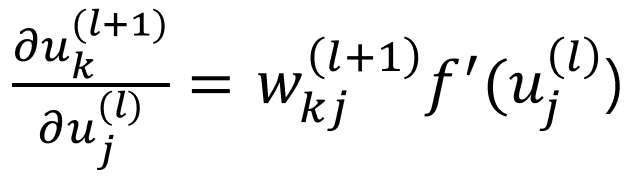

(식 21)

이를 (식 18)에 대입을 하면 아래 식(식 22)이 나옵니다.

(식 22)

(식 22)에서는 좌변을 우변을 통해 계산할 수 있습니다. 즉 더 위층인 l+1층의 노드에 대한 '델타'가 주어지면 l층의 델타는 (식 22)을 통해 구할 수가 있습니다. 이를 아래 그림(그림 4)으로 표현했습니다.

(그림 4)

당연히 (식 22)에서 l을 l+1으로 바꿔써도 성립합니다. 그러므로 출력층인 L층까지 올라가 맨 처음 출력층의 노드에 대한 델타가 계산되어 있으면, (식 22)을 반복 계산하여 어떤 층이든 델타를 구할 수 있습니다. 보시다시피 델타가 순전파와 반대 방향, 즉 출력층에서 입력층 방향으로 전파되기 때문에 '역전파법(backpropagation)'이라고 부릅니다.

 

(식 17)의 1번째 항은 위에 방법으로 델타를 계산하여 구합니다. 2번째 항은 (식 20)에서 l+1를 l층으로 변경한 것으로 부터 구합니다. 이를 통해

 

(식 23)

(식 23)이 나옵니다. 이제 (식 17)에 (식 19)와 (식 23)을 대입하면, 목적하는 미분은 (식 24)로 표현됩니다.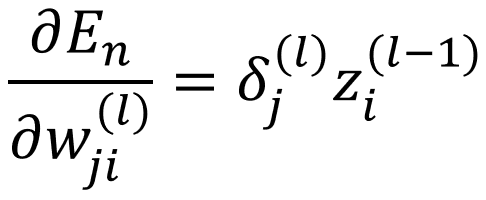

(식 24)

(식 24)을 풀어 설명하자면, l-1번째 층의 노드 i와 l번째 층의 노드 j를 잇는 결합의 가중치에 대한 미분은 노드 j에 대한 델타와 노드 i의 대한 출력 zi의 곱으로 표현할 수 있습니다. 이는 (그림 4)에서 빨간색으로 표시한 선들이 미분을 계산하는데 관여합니다.

 

 

4. 정리

어떤 훈련 샘플(x, d)가 주어졌을 때, 이 샘플에 대한 오차함수 En이 기울기를 지금까지 구해봤습니다. 이를 정리를 해보겠습니다.

 

 

---

제법 어려운 내용이었습니다. 천천히 식들을 따라 계산하다 보면 최종 식을 도출할 수 있을 겁니다.

보시다가 잘 이해가 안되시는 분은 댓글 달아주세요~

감사합니다 :)