[확률적 경사 하강법(SGD)] 5. 과적합 완화(학습을 위한 트릭)

 

안녕하세요. 개알못입니다~~

갑자기 장마가 시작 되었네요 허허

 

오늘은 저번 시간에 이어 과적합을 완화시켜주는 법에 대해 알아보겠습니다 :)

이번 5번째 글을 마지막으로 SGD를 마무리하겠습니다!!

 

---

 

저번 시간에는 규제화를 통해 과적합을 완화시켜주었습니다. 규제화를 크게 3가지로, 가중치감쇠 / 가중치 상한 / 드롭아웃이 있습니다. 그중에서 드롭아웃+가중치 상한을 함께 사용하는 것이 효과가 높음을 보았습니다. 이번 시간에는 학습 시에 적용하는 것만으로도 일반화 성능을 향상시키거나, 학습을 빨리 진행할 수 있게 하는 여러 방법에 대해 알아보겠습니다.

 

 

1. 전처리

 

훈련 데이터에 어떠한 경향이 포함될 때, 이러한 경향이 학습에 방해를 줄 수 있습니다. 이를 제거하기 위해 진처리(Preprocessing) 과정을 거칩니다. 이때 훈련 데이터에 어떠한 전처리 과정을 거친거랑 테스트 데이터 및 추론 시에 입력되는 데이터에도 동일한 전처리 과정을 거쳐야합니다.

 

 

2. 데이터 정규화

 

가장 기본적인 전처리 과정은 데이터 정규화(normalization of data)입니다. 이는 데이터 표준화(standardization of data)라고도 불립니다. 데이터 정규화는 각 샘플 Xn을 "선형 변환"하여 그 성분 단위의 평균과 분산을 구합니다. Xn의 각 성분을 Xni로 한다면, 각 성분 Xni에서 해당 성분의 학습 데이터 전체에서의 평균 averageX를 뺍니다.

 

Xni의 평균 식

Xni의 변환 (1)

 

위에 식처럼 과정을 거치면 변환된 샘플의 평균이 0이 됩니다. 그 후 변환된 Xni를 아래 식처럼 표준편차로 나누어 줍니다.

 

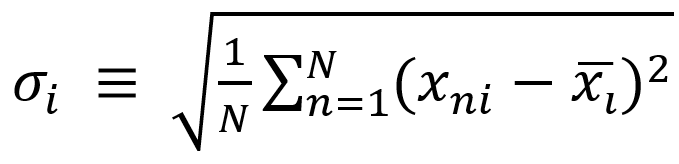
Xni의 표준편차 식

Xni의 변환 (2)

 

이렇게 두번의 변환을 거치게 되면 평균은 0, 분산은 1이 됩니다.

 

간단한 예를 들어 보겠습니다. 샘플 Xn을 1 2 3 4 5로 5개가 들어 있다고 할때 데이터 정규화를 시켜보겠습니다.

 

 

다만 데이터에 따라서 특정한 i 성분만 분산이 0이나 매우 작은 경우가 있는 경우, 그대로 데이터 정규화를 거치면 문제가 발생합니다. 그럴때는 분산 대신 max(분산, 충분히 작은 값)으로 나누거나 분산을 따로 계산하지 않으셔도 됩니다.

 

 

3. 데이터 확장

 

과적합을 일으키는 가장 큰 원인은 훈련 데이터의 부족입니다. 흔히 대량의 샘플을 수집하는 것은 고비용이 들며, 불가능하기도 합니다. 이럴 땐 이미 확보한 샘플 데이터를 일정하게 가공하여 양적으로 물타기하는 법을 데이터 확장(data augmentation)라고 부릅니다. 지도학습에서는 샘플 (x,d) 에 관하여 새로운 샘플 (x',d)를 만듭니다.

 

보통 샘플의 분포 양상을 예상할 수 있는 이미지 데이터에서 데이터 확장이 자주 적용이 됩니다. 같은 카테고리의 물체 이미지이라면 이미지에 어느정도의 변화를 가해도 타당한 훈련 샘플이 만들어 집니다. 예컨데 이미지의 평행이동, 거울상 반전, 회전등의 기하학적 변환이나 픽셀의 명암값이나 색의 변동 등을 가하여 새로운 샘플을 만들 수 가 있습니다. 또한 가우스 분포에 따르는 Random Noise를 일괄적으로 적용할 수 도 있습니다.

 

 

4. 여러 신경망의 평균

 

또다른 방법은 다수의 서로 다른 신경망을 조합하는 겁니다. 다시 말해, 같은 입력을 여러 개의 신경망의 입력하여 얻어진 출력의 평균을 응답으로 여깁니다. 물론 각 신경망은 입력층와 출력층의 구성은 같습니다. 신경망뿐만 아니라 머신러닝 전반적으로 사용되는 이 방법을 모델 평균(model averaging)라고 부릅니다. 이는 학습 시에 각 신경망을 서로 '독립적'으로 훈련시킵니다. 이는 규제화 파트에서 말했던 드롭아웃에 경우, 신경망 하나를 사용해서 실질적으로 여러 개의 신경망에 모델 평균을 적용하는 것과 같은 효과임을 볼 수 있습니다.

 

 

5. 학습률의 결정 방법

 

경사 하강법에서는 파라미터의 갱신 정도를 학습률을 톨해 조절합니다. 그러기에 학습률을 어떻게 설정할지가 굉장히 중요한 부분입니다. 학습률을 결정하는 여러가지 방법이 있는데

 

5.1)

첫번째 방법은 학습 초기에 값을 크게 설정했다가 학습의 진행화 함께 학습률을 점점 줄이는 법입니다. 예컨데, 처음에 상수 ε=ε0 을 설정하고 학습이 진행되면 그 값을 ε = ε0 / 10 으로 줄여 파라미터 갱신을 계속하며 이를 반복합니다. 또는 학습률을 파라미터 갱신 회수에 비례하여 작아지도록 ε = ε0/αt 로 제어합니다.

 

5.2)

두번째 방법은 신경망의 모든 층에서 같은 학습률을 사용하는 것이 아니라 층마다 서로 다른 값을 사용하는 것입니다. 각 층의 가중치 업데이트 속도가 비슷하게 가중치를 설정하는 것이 좋다고 알려져 있습니다. 더불어 로지스틱 함수처럼 치역이 제한된 활성화 함수일때 더욱 효과적입니다. 예컨데, 출력 방향에 가까운 얕은 layer에는 학습률을 작게, 입력에 가까운 layer에는 크게 잡는 경우입니다.

 

5.3)

또다른 방법에는 학습률을 자동적으로 변화시키는 법이 있는데, 이 중에서 AdaGrad가 대표적입니다.

 

라고 할때, 일반적인 경사하강법에서는 갱신 성분 i가 아래 처럼 나타내지만

일반적인 경우

AdaGrad의 경우에는 아래처럼 나타냅니다.

AdaGrad

 

직관적으로 AdaGrad식을 보면, 자주 나타나는 기울기의 성분보다 드물게 나타나는 기울기의 성분을 더 중요시하여 파라미터를 갱신합니다.

 

6. 모멘텀(momentum)

 

경사 하강법의 수렴 성능을 향상시키는 방법 중 모멘텀(momentum)이라는 방법이 있습니다. 모멘텀은 가중치의 갱신 값에 이전 갱신 값의 일정한 비율을 더하는 방법입니다.

 

미니 배치 t에 대한 가중치 갱신 값을 아래 식이라 한다면,

미니 배치 t에 대한 업데이트는 아래 식과 같다.

μ는 더할 값을 비율로 제어하는 하이퍼 파라미터(hyper-parameter)입니다. 이 값은 0.5~0.9 사이의 값을 가집니다.

 

아래 사진을 보면 왼쪽은 모멘텀이 적용이 안된 오차함수의 형상이고, 오른쪽은 모멘텀이 적용된 것입니다. 사진처럼 골짜기가 깊기 때문에, 조금이라도 골짜기 바닥에서 나오면 왼쪽처럼 골짜기와 직교하는 방향으로 큰 기울기가 생깁니다. 그 결과 가중치는 매번 골짜기와 직교하는 방향으로 갱신되어 경로가 지그재그 모양으로 되어 제대로 탐색하지 못하게 됩니다.

 

source : https://www.quora.com/What-does-momentum-mean-in-neural-networks

 

모멘텀은 이런 문제를 해결하고 오른쪽 그림처럼 골짜기 방향에 따라 골짜기 바닥을 효율적으로 탐색하게 해줍니다.

미니배치 t에 대한 갱신 식을 다시 정리해보면 아래와 같습니다.

이때

이 값을 '가중치의 갱신 양의 갱신 양'으로 생각할 수 있습니다.

갱신양이 과거의 갱신양의 가중평균이 되기 때문에, 골짜기와 직교하는 방향의 갱신양은 자연스럽게 평균화 중에 상쇄되어 가중치가 수정되는 경로가 지그재그 되지 않습니다. 

 

---

이외에도 가중치의 초깃값을 결정하는 방법이나 훈련 샘픔을 어떤 순서로 추출할 것인가에 따른 방법 등이 있습니다.

과적합을 완화하는 여러가지 방법들을 살펴보고 현재 모델에서 가장 적절한 방법을 채택해서 적용하면 되겠습니다!!

 

지금까지 함께 해주셔서 감사합니다 ~

질문과 댓글은 언제나 환영입니다 :)