[확률적 경사 하강법(SGD)] 3. 미치배치, 일반화 오차

안녕하세요~

 

날씨가 많이 덥네요!! 이어서 계속 설명하겠습니다 :)

---

1. 미니배치(minibatch)

 

큰 규모의 신경망 학습은 계산비용이 대규모로 발생합니다. 그러기에 효율적인 수치 계산을 하기 위해서는 행렬 계산 자원이 꼭 필요합니다. 즉, 샘플 한개 단위가 아니라 여러 개의 샘플을 하나의 작은 집합으로 묶어서 집합 단위로 가중치를 업데이트를 해줍니다. 이러한 작은 집합을 미니배치(minibatch)라고 합니다.

 

 

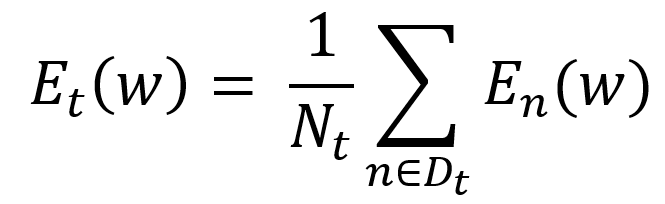
위에 식에서 Dt는 몇 개의 샘플 집합을 지니고 있는 미니배치입니다. 첨자로 써져있는 n E Dt의 의미는 t번째 마다 샘플 집합의 변화입니다. 그리고 미니배치가 포함하는 모든 샘플에 대한 오차를 계산한뒤, 그 기울기 방향으로 파라미터를 갱신합니다.

 

Nt는 해당 미니개수가 가지고 있는 샘플의 개수입니다. Nt로 나눠주는 것을 정규화라고 하는데, 이를 통해 미니배치의 샘플 수를 변화시킬때마다 학습률을 조정해야하는 수고를 없앨수가 있습니다.

 

일반적으로 미니배치는 SGD의 장점을 고려하자면 10~100개 샘플로 결정이 되고, 학습을 시작하기 전에 고정시켜줍니다. 저번에 살펴본 다클래스 분류 문제의 경우 미니배치 간의 가중치 업데이트 값을 일정하게 하기 위해서는 미니배치마다 각 클래스의 샘플이 하나 이상 들어가게 설정하면 됩니다.

 

미니배치의 크기를 크게 할수록 각 배치마다 계산되어지는 기울기의 값이 일정해집니다. 그러기에, w의 갱신이 안정화 되고 학습률을 크게 높일 수 가 있습니다. 이를 통해 학습의 속도 또한 높아집니다. 물론 미니배치의 크기와 학습률이 1:1 비례관계는 아닙니다 :)

 

---

2. 일반화 오차(generalization error)

 

이전까지는 훈련 데이터(training data)의 오차만 다루었습니다. 사실 더 중요한 것은 훈련 데이터보다 앞으로 미지의 샘플에 대한 정확한 추정입니다. 이를 일반화 오차(generalization error)라고 부르고 테스트 오차(test error)라고도 합니다. 일반화 오차를 되도록 작게하는게 목표이지만, 일반화 오차 자체가 기댓값이기 때문에 훈련오차처럼 계산할 수 없습니다. 그리므로 훈련 데이터와 다른 별도의 샘플 집합은 훈련 오차와 같은 방법으로 계산한 오차를 기준으로 합니다.

 

source : https://www.researchgate.net/figure/Training-error-and-cross-validation-error-as-a-function-of-model-complexity_fig3_222344717

 

위에 그래프는 학습곡선(learning curve)라고 부릅니다. 훈련오차와 테스트오차가 학습에 의한 파라미터 변화에 따라 달라지는 모습을 의미합니다. 학습초기에는 테스트오차가 훈련오차와 마찬가지로 감소하다가 학습 도중에 갑자기 증가함을 볼 수 있습니다. 이렇게 훈련오차와 테스트 오차가 심하게 달라지는 값을 갖게 되는 상태를 과적합(overfitting) 혹은 과학습(overlearning)이라 부릅니다.

 

테스트 오차와 일반화 오차가 서로 비슷한 값을 갖고 테스트 오차가 최소가 되는 상태가 가장 이상적입니다. 그러나 과적합이 일어나게 되면 오히려 학습을 방해하기 때문에 그 시점부터 학습을 종료합니다. 이를 조기중단, 조기종료(early stopping)이라 부릅니다.

---

앞으로 과적합을 줄일 수 있는 여러 방법에 관하여 다음시간에 다루어 보도록 하겠습니다.

질문과 댓글은 언제나 환영입니다 :)