[확률적 경사 하강법(SGD)] 1. 경사 하강법

안녕하세요. 개알못입니다~~

 

이번 시간에는 딥러닝에서 자주 쓰이는 확률적 경사 하강법에 대하여 이야기 하겠습니다. 총 6~7번의 포스팅으로 마무리 될 것으로 예상됩니다.

 

---

1. 앞먹임 신경망의 사전 지식

 

1.1 앞먹임 신경망

 

경사 하강법에 들어가기 앞서, 앞먹임 신경망의 대한 사전 지식일 필요합니다. 간단히 설명하면,

 

앞먹임 신경망 학습 : 주어진 다음의 훈련 데이터로부터 계산되는 오차함수 E(w)를 신경망의 파라미터 w에 대하여 최소화하는 과정

 

 

1.2 훈련 데이터

 

하나의 입력 x에 대한 출력을 d 일때, 이러한 입출력이 쌍으로 있는 경우 아래 처럼 표현합니다.

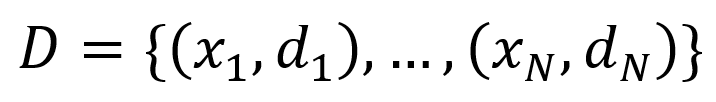
각 입출력 쌍 (x, d)를 훈련 샘플(training samples)이라, 전체 집합 D를 훈련 데이터(training data)라고 부릅니다. 이를 앞으로 회귀 문제와 다클래스 분류 문제에 적용할 것입니다.

 

 

1.3 회귀 문제의 오차함수

 

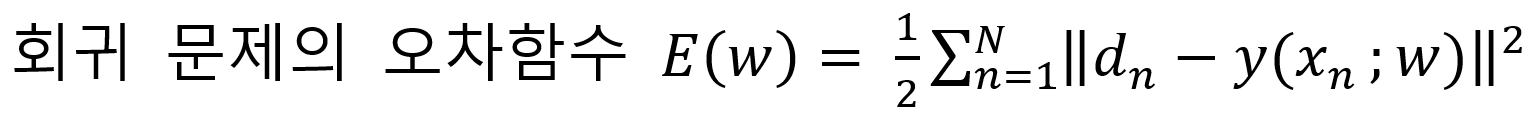
여기서 목표 출력인 dn은 임의의 실수값인 벡터입니다.

 

 

1.4 다클래스 분류 문제의 오차함수

 

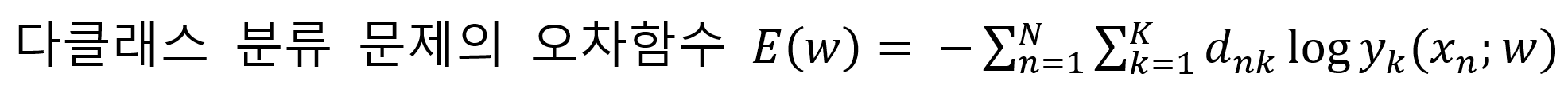
여기서도 목표 출력인 dn은 

클래스 수와 같은 수의 성분을 가진 벡터입니다. 또한 정답 클래스에 대응하는 성분 하나만 1이고, 나머지 성분은 0입니다. 예를 들어, 해당 숫자가 0~9 중 어느 클래스인지 속하는 문제에서는 dn = [0001000000]T 로 나옵니다.

 

회귀문제와 다클래스 분류 문제의 오차함수의 도출 식은 추후에 다시 포스팅해서 다루겠습니다.

---

2. 경사 하강법에 대하여

 

2.1 Local Minimum

 

학습의 목표는 선택한 E(w)에 최솟값을 주는

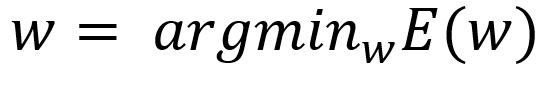
w를 구하는 것입니다. 그렇지만 흔히 E(w) 단순한 Convex Function(볼록함수)가 아니기 때문에, Global minimum을 직접 구하기가 어렵습니다. 그러므로 대신 E(w)의 Local Minimum w를 구하는 것은 그리 어렵지 않습니다. 

source : https://ko.wikipedia.org/wiki/%EA%B7%B9%EA%B0%92

그러나 E(w)의 Local Minimum w은 일반적으로 다수 존재하기 때문에, 이렇게 구한 극소점이 Global minimum 이기는 쉽지않습니다. 그럼에도 Local Minimum의 w에서의 E(w)이 충분히 작다라면, 앞서 살펴본 회귀문제와 클래스 분류 문제에서도 잘 풀 수 있습니다.

 

 

2.2 경사 하강법 (gradient descent method)

 

Local Minimum을 구하는 법은 어떤 초기 점으로 출발하여 w를 되풀이하여 갱신하는 겁니다. 그 중에서도 가장 간단한 법이 경사 하강법(gradient descent method)입니다. 이 중 경사 하강법의 기울기(gradient)은

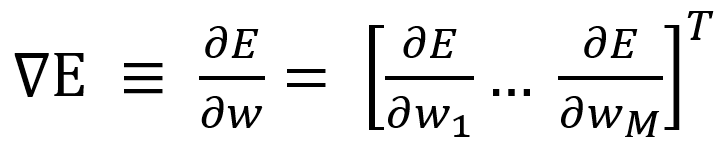
M은 w의 성분 수이다.

경사 하강법은 현재의 w를 음의 기울기 방향으로 움직이고, 이를 되풀이하여 갱신합니다.

즉 초깃값인 w(1)가 결정된 이후 t 값에 변화를 주어 w(2), w(3)... 진행합니다.

 

 

2.3 학습률 (learning rate)

 

이때 E 모양이 w의 갱신량의 크기를 결정하는데, 이를 learning rate(학습률)라고 부릅니다. w(t)에서 learning rate 가 충분히 작다라면, E(w(t))의 값이 감소되고, 계속 반복계산 할수록 극소점에 도달하게 됩니다.

그러나 learning rate 가 너무 작다라면, w가 한 번 갱신 될 때 변화량이 너무 적어, 반복 횟수가 많이 필요하고 학습시간이 늘어나게 됩니다.

 

---

다음 포스터에서는 '확률적 경사 하강법'에 관해 이야기 하겠습니다.

질문과 댓글은 언제나 환영합니다 :)